Optimization Methods for More Effective Pricing Management

When you walk down a grocery store aisle as a customer, a mosaic of products and prices greet you. How that retailer is priced on the selection of goods that you purchase, especially the ones on which you care most about receiving value, drives your price perception as well as overall engagement with that store.

For a category manager in the grocery industry, simultaneously meeting the diverse needs of customers as well as maintaining financial performance of their category becomes a complex undertaking that entails finding balance amongst often competing objectives.

A recent case study discussed some of the complexity associated with deploying the most effective pricing and how optimization can be used to improve both customer engagement as well as business results. Today, we are going to dive into two of the technical components of optimization that allow for improvement simultaneously across customer-focused and business-focused objectives.

Mathematical optimization can be conceptualized as the combination of three main elements: an objective function, decision variables, and constraints. The purpose of an optimization program is to find the maximal (or minimal) possible value of its objective by searching for the ideal decision variable values, while also respecting the constraints that are in place.

The objective function provides the measure that is being maximized and represents the “goal” of the optimization. For example, objectives in the retail industry may be increasing total sales velocity or increasing some quantifiable measure of customer engagement.

Decision variables are the values that are changed to maximize the objective function. In an everyday pricing optimization, the prices of each of the different products in a category would be its decision variables.

Constraints allow for business logic to provide bounds on the solution. These could include elements such as ensuring that the larger-sized variety of a product carries a lower equivalized unit price than its smaller-sized counterpart or maintaining a certain price gap between premium and value brands.

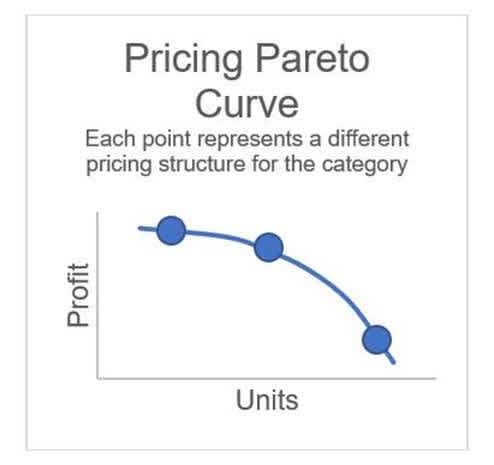
Within optimization, improvements in one measure may often come at the expense of other measures. Such tradeoffs can be visualized through a Pareto frontier (or “Pareto curve”), which exhibits the range of potential optimal solutions if one were to incrementally shift the proportion of value the model places on one measure to the other. A Pareto curve may be generated by running a series of optimizations, incrementally changing the constraints on the tradeoff variables of interest.

For pricing, one common Pareto view compares total profit vs. units sold – measures which inherently have some tradeoff. For a mini example, this could be generated by running three optimizations where the objective function quantifies total units, and a lower-bound constraint on profit is stepped up with each iteration. In this example, let’s say the iterations specify that profit may not decrease more than -5%, -3%, and -1%, respectively, from the model’s starting point.

In practice, a Pareto curve summary becomes a great visual tool for category managers to understand opportunities in their categories and better balance customer engagement with business financials.

A multi-objective optimization program builds upon the concept of Pareto optimality and involves the formulation of an objective function that combines multiple success measures into a single expression.

In pricing optimization, where objectives such as unit volume, sales, and profit may be projected from similar calculations, such a transformation is possible and unlocks a handful of benefits for business users.

In this approach, a Pareto curve can be generated by varying a weighting of each measure in the objective function, while keeping business-facing constraints consistent. This can result in:

• Better balance of customer and business objectives leading to higher overall benefit of the optimization solution, and

• Faster, more efficient processing to achieve the best solutions, which decreases the amount of time needed to understand the category opportunity

It also gives business end users the ability to intuitively alter the weighting to adapt to changing business needs in their category. For example, a category manager may want to increase customer engagement by driving unit volume. A weighting of 70% units, 15% sales, and 15% profit might accomplish this. If the category is ahead of unit volume targets later in the year and the category manager is looking to increase profitability, a weighting of 30% units, 30% sales, and 40% profit may increase margins in the category, while also providing some degree of customer protection on the products they care about the most.

An overall benefit of a multi-objective optimization approach is that the program will accomplish this balance in a customer-first manner (assuming sufficient weighting is placed on customer-focused metrics such as units, trips, or households). This is accomplished as the optimizer drives its objective through a blend of lowering prices on items that customers value the most, while realizing margin enhancement on products that are less price sensitive.

Within an increasingly complex retail environment that benefits from data driven decision making, pricing optimization is a tool that bridges the gap between more effective category management and the customer.

By taking a customer centric approach through optimization, you are helping to ensure that as customers walk down a grocery aisle and place items into their basket, they are excited about the prices they see and have reason to return week after week.

Pareto frontiers and the multi-objective approach bring this customer centric view directly to category managers, at the time that important pricing decisions are being made. It is a cornerstone of effective pricing programs and a building block to long-term customer engagement.